洛谷笔记 - P1065 [NOIP2006 提高组] 作业调度方案

发表于 更新于 本文字数： 1.6k 阅读时长 ≈ 6 分钟

题面很长，读了很久，没读懂，遂弃键盘，睡之

才怪！

不过也起码花了我一上午的时间搞……

太痛苦了！太痛苦了！

题目描述

我们现在要利用 mm 台机器加工 nn 个工件，每个工件都有 mm 道工序，每道工序都在不同的指定的机器上完成。每个工件的每道工序都有指定的加工时间。

每个工件的每个工序称为一个操作，我们用记号 j-k 表示一个操作，其中 jj 为 11 到 nn 中的某个数字，为工件号；kk 为 11 到 mm 中的某个数字，为工序号，例如 2-4 表示第 22 个工件第 44 道工序的这个操作。在本题中，我们还给定对于各操作的一个安排顺序。

例如，当 n=3,m=2n=3,m=2 时，1-1,1-2,2-1,3-1,3-2,2-2 就是一个给定的安排顺序，即先安排第 11 个工件的第 11 个工序，再安排第 11 个工件的第 22 个工序，然后再安排第 22 个工件的第 11 个工序，等等。

一方面，每个操作的安排都要满足以下的两个约束条件。

  1. 对同一个工件，每道工序必须在它前面的工序完成后才能开始；

  2. 同一时刻每一台机器至多只能加工一个工件。

另一方面，在安排后面的操作时，不能改动前面已安排的操作的工作状态。

由于同一工件都是按工序的顺序安排的，因此，只按原顺序给出工件号，仍可得到同样的安排顺序，于是，在输入数据中，我们将这个安排顺序简写为 1 1 2 3 3 2。

还要注意，“安排顺序” 只要求按照给定的顺序安排每个操作。不一定是各机器上的实际操作顺序。在具体实施时，有可能排在后面的某个操作比前面的某个操作先完成。

例如，取 n=3,m=2n=3,m=2，已知数据如下（机器号 / 加工时间）：

工件号 工序 11 工序 22
11 1/31/3 2/22/2
22 1/21/2 2/52/5
33 2/22/2 1/41/4

则对于安排顺序 1 1 2 3 3 2，下图中的两个实施方案都是正确的。但所需要的总时间分别是 1010 与 1212。

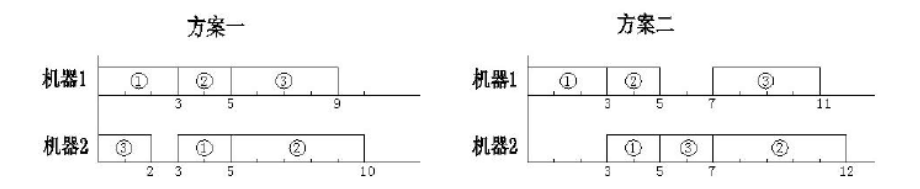
当一个操作插入到某台机器的某个空档时（机器上最后的尚未安排操作的部分也可以看作一个空档），可以靠前插入，也可以靠后或居中插入。为了使问题简单一些，我们约定：在保证约束条件（11）（22）的条件下，尽量靠前插入。并且，我们还约定，如果有多个空档可以插入，就在保证约束条件（11）（22）的条件下，插入到最前面的一个空档。于是，在这些约定下，上例中的方案一是正确的，而方案二是不正确的。

显然，在这些约定下，对于给定的安排顺序，符合该安排顺序的实施方案是唯一的，请你计算出该方案完成全部任务所需的总时间。

输入格式

第 11 行为两个正整数 mm, nn，用一个空格隔开，
（其中 m(<20)m(<20) 表示机器数，n(<20)n(<20) 表示工件数）

第 22 行：m×nm \times n 个用空格隔开的数，为给定的安排顺序。

接下来的 2n2n 行，每行都是用空格隔开的 mm 个正整数，每个数不超过 2020。

其中前 nn 行依次表示每个工件的每个工序所使用的机器号，第 11 个数为第 11 个工序的机器号，第 22 个数为第 22 个工序机器号，等等。

后 nn 行依次表示每个工件的每个工序的加工时间。

可以保证，以上各数据都是正确的，不必检验。

输出格式

11 个正整数，为最少的加工时间。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
2 3
1 1 2 3 3 2
1 2 
1 2 
2 1
3 2 
2 5 
2 4

样例输出 #1

1
10

提示

NOIP 2006 提高组 第三题

代码

编写代码的过程中参考了一些题解内容 [1]。

主要思路为对同一零件的前后加工进行限制，同时限制不同机器的时间轴上的同一个大的时间分段内每台机器最多制作一次工件。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
// Problem: P1065 [NOIP2006 提高组] 作业调度方案
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1065
// Memory Limit: 128 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<iostream>
#include<cstring>
using std::cin;
using std::cout;
using std::endl;
bool m_proc[21][100001]; //各机器各时间点的使用情况
int main(){
    struct{
        int m_id,ntime; //机器ID、工件加工时间
    }gj[21][21];
    memset(gj,0,sizeof(gj));
    int m,n; //机器数、工件数
    cin>>m>>n;
    int srt[401]; //操作顺序
    for(int i=1;i<=m*n;i++){
        cin>>srt[i];
    }
    for(int i=1;i<=n;i++){
        for(int o=1;o<=m;o++){
            cin>>gj[i][o].m_id;
        }
    }
    for(int i=1;i<=n;i++){
        for(int o=1;o<=m;o++){
            cin>>gj[i][o].ntime;
        }
    }
    int lptime[21],ans=0,n_step[21]; //各零部件最后处理时间, 答案输出
    memset(lptime,0,sizeof(lptime));
    memset(n_step,0,sizeof(n_step));
    for(int i=1;i<=m*n;i++){
    	int num=srt[i];
        n_step[num]++;
        int m_spare=0;
        int m_id=gj[num][n_step[num]].m_id;
        for(int o=lptime[num]+1;;o++){
            if(m_proc[m_id][o]==0){
                m_spare++;
            }else{
                m_spare=0;
            }
            if(m_spare==gj[num][n_step[num]].ntime){
                for(int p=o-m_spare+1;p<=o;p++){
                    m_proc[m_id][p]=1;
                }
                if(o>ans){
                    ans=o;
                }
                lptime[num]=o;
                break;
            }
        }
    }
    
    printf("%d\n",ans);
    return 0;
}

后记

这玩意绝对是我目前见过最绝的一篇模拟题，几个月前看到的时候险些给自己绕进去。

关于我为什么要做这道题这个问题，主要还是前些天学校网络技术协会的技术团队要面试，然而昨天晚上轮到我的时候由于信竞知识已经晾在一边数月之久（其实没有数月，基本从遣返回家开始就没碰过 CPP 编程相关的东西了）喜提 “等通知” 的优异成绩（其实本来也没学会多少知识，时间复杂度不会算、快排犯迷糊、深搜说不出原理……），危机意识上来了，遂做此题，以此勉励。

比东北平原都平的做题曲线

不过我估计返校之前可能又会回归颓废状态吧

  1. 1. 题解 P1065 【作业调度方案】 - brealid 的博客: https://www.luogu.com.cn/blog/_post/105786 ↩